Finding the length of Comet Neowise's tail

Discussions
#1

We did some basic math at the club today to guess the length of Comet Neowise’s tail. After a bit of thinking, we realised this was possible with some high school trigonometry. This would have been an excellent activity to do with school kids in person but…thanks COVID-19. I am sharing it here so that any kids at home who are going restless can try this and see how trigonometry is used in real life scenarios.

Anyway, this is a rough way to go about it. You will first have to figure out the apparent length of the comet’s tail as seen from the Earth. You can use your fingers to do this. If the comet is currently not visible from your place, any reliable online source can be used. This NASA blog mentions that it’s about 7 degrees long. We also know that the distance between the comet and the Earth during its closest approach to the Earth is 0.69AU, which is about 103,222,531 kilometers.

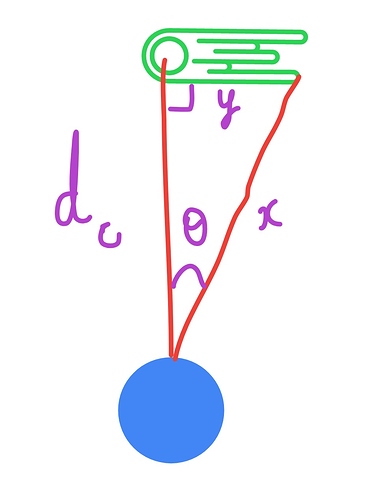
Now let’s try and visualise this.

My amazing drawing skills showing off the comet and the earth
My amazing drawing skills showing off the comet and the earth966×1268 62.6 KB

Here, θ is the length of the tail that we took to be 7 degrees. dc is the closest distance of the comet to earth(103,222,531km), x is the length of the hypotenuse and y is the length of the comet.

Method 1

cos θ is given by dc / x.

Substituting for θ and dc, we get

cos 7 = 103,222,531 / x

Now, cos 7 is 0.99254615. Substituting, we get

x = 103,997,714

Now, from the famous Pythagoras theorem, we have

x2 = dc2 + y2

which can be rearranged as,

y2 = x2 - dc2

Substituting the values and taking square roots on both sides, we get the size of the comet’s tail y to be

y = 12,674,134 km

Therefore, the tail of the comet is about 12 million kilometers long if the tail was 7 degrees wide during it’s closest approach to Earth.

Method 2

tan 7 = y / dc

Therefore, y = tan 7 * dc

Substituting, we get y = 0.12278456 * 103,222,531

y = 12,674,133 km

which is again 12.6 million kilometers.


This post has a lot of assumptions and does not give an accurate size of the comet’s tail. For example,

  1. The comet is not aligned in a perpendicular angle like in the figure wrt Earth.
  2. The tail itself is curved in reality. It’s not straight as shown here.
  3. The comet’s tail was not 7 degrees on the day of its closest approach to the Earth.

However, I feel these assumptions are needed to make the problem approachable, at least for kids. What do y’all think? Do you have any other approaches to this problem?

6 Likes